Skip to content

Calculadora de Subnetting Método Optimista | Grandes Redes

La calculadora de subnetting del método optimista es una herramienta en línea gratuita que permite dividir un espacio de red en otras grandes subredes y, una vez que las obtiene, puede aplicar técnicas VLSM o FLSM. Entonces, antes que nada, calcula desde una dirección de red principal como 172.16.0.0/12 los otros grupos con su dirección de red. Y luego, para cada subred, puede aplicar FLSM o VLSM para obtener sus respectivas subredes.

Ya veremos en el otro método, el pesimista que al final es cuando generaremos el espacio final y no en cada bloque de nubes. Por lo tanto, el procedimiento computacional de uno y otro difiere en los espacios libres y en como manejarlos y de esta manera hacer mas eficientes nuestras subredes.

Si aparece en blanco, espere a que acabe de cargar la calculadora para poder usarla.

Video explicativo del uso de la Calculadora de Método Optimista:

Índice del artículo

    Ejercicios resueltos – Paso a paso

    Cómo usar la calculadora de subnetting método optimista

    Ingrese la dirección y el prefijo de la red principal, como 172.16.0.0/12. Luego, para cada grupo de red ingrese el número de redes y hosts/red. Una vez, tiene sus grupos de red, debe ingresar grupos de enrutadores. Imagine que tiene dos grupos, entonces solo necesitará un grupo de enrutadores. De forma predeterminada, todos los nombres se agregan aleatoriamente, puede cambiarlos y su tamaño en cualquier momento. Cuando haya terminado, presione el botón CALCULAR.

    Resultados que puede obtener con la calculadora de subnetting de método optimista

    • Resultados de las ecuaciones: obtendremos una tabla donde para cada grupo calcularemos la X y la N y los ordenaremos por sus totales.
    • Rango de nuestra red de partida.
    • Información de los grupos: bits/host, formato de la IP, nueva máscara de red, dirección de red y la dirección de broadcast.
    • Espacio global LIBRE.
    • Calcularemos cada problema y aplicaremos FLSM o VLSM dependiendo de las especificaciones del problema.
    • Por cada subproblema obtendremos la primera y última dirección de red y la dirección de broadcast de las subredes. Además, hay un filtro para buscar las direcciones que se deseen y poder comprobar el formato de la IP, el espacio libre, el tamaño de bloque y la nueva máscara de red.
    • Espacio global LIBRE que ha sobrado.
    calculadora método optimista
    Ejemplo de la Calculadora Método Optimista

    Explicación del problema del grupo de redes

    Partimos de un espacio común y de un esquema de red como podría ser el siguiente:

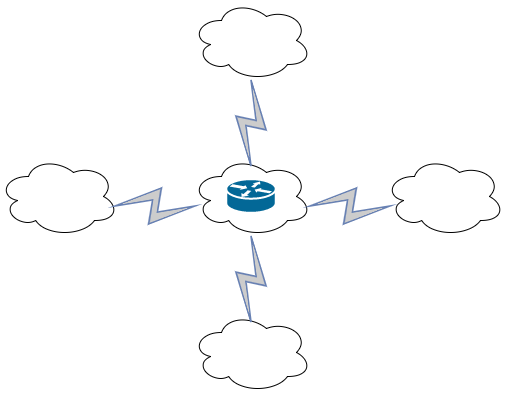
    esquema de red metodo optimista
    Esquema de red del método optimista

    Tenemos que cada nube colindante tiene sus redes y sus hosts/red, mientras que la nube del centro tiene las conexiones P2P. Por lo tanto, tenemos 5 nubes, 4 grupos y la nube de interrelaciones.

    Partiendo del ejemplo anterior, habría que calcular para cada nube, la ecuación de la X y la ecuación de la N de la siguiente manera:

    min(x)
2x >= hosts + 2
    min(n)
2n >= redes

    A continuación, hay que sumar dichas ecuaciones para poder ordenar los grupos. En el grupo de interrelaciones si no nos dice nada el enunciado, las redes serán P2P (2 hosts por red). Para calcular su N hay que suponer que hay tantas conexiones P2P como redes en total, es decir, sumaríamos todas las redes de todas las nubes.

    Luego ordenaremos cada grupo en función de 2 valores: el de la suma y si la suma son cantidades iguales, empezamos con el que tenga una X mayor. Si la X también es igual, nos fijamos en el número de hosts/red.

    Con este método si tenemos 5 bloques, al final de cada uno nos aparece un espacio libre porque tenemos direcciones de sobra. No obstante, en el pesimista, cuando pasamos al siguiente grupo lo empezamos utilizando el espacio desaprovechado (no podemos dejar ningún bit en blanco).

    Y al final, calcularíamos cada grupo mediante FLSM o VLSM.